|
下圖中正方形的邊長是10厘米,三角形甲的面積比三角形乙的面積少20厘米,求線段AB的長��。 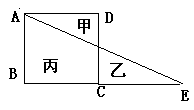
解法一: 思路:乙三角形任何一條邊長都不知道����,但和甲有共同聯(lián)系的就是白色部分,甲組成了正方形��,乙組成了個(gè)更大的三角形�����。甲和乙同時(shí)加上相等面積��,原來的差不變�����,這樣就可以求出乙的大三角形面積�����,從而得到ab的長��。 解法:因?yàn)?nbsp; 乙大三角形面積—正方形面積=20平方厘米 則有��,大三角形面積=10×10+20=120平方厘米 大三角形的底邊長為10�,則根據(jù)面積公式得出 高(即BA的延長線)=120×2÷10=24 則AB=24-10=14厘米
解法二: 解:連接DE 乙比甲面積大10平方厘米 所以△DCE比△ADE大10平方厘米(同時(shí)增加了一個(gè)三角形面積) 即CD*CE/2-AD*CD/2=10 CE-AD=2 所以CE=12cm |